by Bradley Knockel
My main goal is to show that statistical thinking is very difficult. Our human brains are terrible at it. Our brains are naturally bad at any sort of careful/scientific/analytical thinking, and thinking about statistics may be the most challenging. Luckily, the brain has the ability to learn, and hopefully math and science has been part of your school life for many years when you were younger. However, because statistics is so subtle and challenging, we must learn a lot so that we are not duped by misleading statistics.
Once we finally understand how stupid the human brain is, then we can begin to compensate for it. We will no longer be easily and constantly duped by the media, casinos, and politicians.
Let's begin by reading this great Cracked article about seemingly simple statistical situations with very surprising results.
Seriously, read it. It's enlightening and hilarious.
Now that you've read it, here are some Wikipedia articles explaining some of these situations in more detail...
Boy or Girl paradox
Monty Hall problem
Birthday problem
Is this stuff confusing and nuanced? Yes! At first, these situations seem simple. The important lesson here is that our human brains are stupid. We cannot trust our instincts. Before our globally interconnected technological society, humans lived in small groups. Our brains are good in these small groups where common sense is valid. If a lion might be around the corner, who cares about calculating the exact probability!? Do not round that corner and go around the other corner! Life is now more complex, and logical thinking is needed when voting, making decisions about technology, and making decisions that affect the large scale. We must well know that our brains and common sense fail us if we wish to not be wrong about so many things. We must think carefully and logically if we wish to have an opinion on any large topic. If, instead of worrying about large topics, we prefer to enjoy only the more traditional aspects of life—food, music, hiking, friendships, etc.—we must then be sure to not vote until we also think carefully about the larger topics, and we must not ignore the advice of doctors, lawyers, scientists, etc. who do worry about the large topics.
For more practical examples, let's think about being sick and getting results from a lab test. There are surprising subtleties when interpreting the results! Do you still trust your common sense before it is guided by careful thinking? The following video shows how easy it is to lie with statistics in the courtroom.
The news media, especially the 24-hour TV networks, have the primary goal of getting viewers. To do this, many stories are sensational. For example, a plane crash is very sensational, so people who think based off of sensation avoid airplanes for safety reasons. However, deaths per mile are far less when flying vs. driving, so, given a trip with fixed mileage, a person should certainly choose flying if safety is the concern (avoiding flying for a fun road trip is a fine reason!). But facts are not as entertaining, so the news media focuses mostly on the horrible images of any plane crash. While more common, car crashes are boring and are not shown or discussed by the media. By the way, interstate driving is much safer than city driving.
Of course, there is nothing abnormal with feeling that flying is scary. However, we must understand that our brains are stupid and, for our own safety (and to save money if only one or two people are traveling), choose to fly regardless of our feelings. Fear must be overcome! If you truly have a crippling fear of flying, driving may be best, but maybe try to master your reactions sooner rather than later?
Are you in the United States and are afraid of dying? Maybe you should look at this to see what we can do to lower our chances. Go to the section that breaks down deaths in the US by age. Drugs are a leading cause of death. Hopefully you do not have to worry about this for yourself. Car accidents are a main threat to young people (largely due to drunk driving, not wearing seat belts, and texting), followed by guns (including suicides). While the media may try to make us scared of terrorists to boost their viewership, we are far more likely to die drowning or in a fire than by a terrorist (even if we include domestic terrorism such as the Oklahoma City bombing). The United States government has done and is actively spending much money and lives to keep us safe (and perhaps also much that makes us no safer).
The brain naturally finds outliers (rare instances) interesting and naturally believes that it knows more than it does. A few plane crashes or terrorist attacks suddenly make us afraid of things that are not a huge concern. But there are worse consequences to our brains being stupid. Unconscious biases are the biases that every single human being has that fuel much discrimination and stereotypes. The brain automatically takes information from a few outliers from a group, then it assumes that any other person from that group is the same. For example, it is well known that identical résumés sent out differing only in the person's name get a much higher response rate if the name is white and male, even if the hiring manager is black and female. The problem is that most of us have the subconscious idea that certain types of people are not good employees in spite of the evidence of them having identical résumés. Biases may sometimes be helpful when making quick decisions, but making large decisions like who to hire are sadly also affected by unconscious biases. Does the media ever mention this even though it is the core issue involved in most of its racial stories? Only very rarely. The media on both sides of the issue instead usually prefers to stir the pot to get viewers in the style of Jerry Springer, creating a population of people who are far from having moderate beliefs. A person who thinks statistically and who is aware of their brain's shortcoming when it comes to making large decisions can overcome the noise from the media and do small things like redact the names on résumés until the interview phase.
Let's take crime in the black and Hispanic communities in the United States as an example of thinking statistically. First let's naively take a first look at some data. Black and Hispanic Americans commit about 37% of the violent crimes, while they make up about 25% of the population. According to some people, we should clearly be afraid of people who are black or Hispanic! Let's consider two more very important statistics. The chances that a black or Hispanic person will commit a crime in any year is only 1%. You see, our brains take the violent outliers and generalize even though nearly all people—regardless of race—are nonviolent. Also, people who are black or Hispanic are approximately twice as likely to be in poverty in the United States than white people, and if you are lucky to not live in an area of poverty, your chances of experiencing or committing any violence go down regardless of the racial demographics of where you live. By the way, the chances of a criminal living in poverty going to jail (as opposed to getting off) goes up.
Perhaps now the important question is: why are blacks and Hispanics more likely to be in poverty? Historically, many laws have even recently excluded black people from accessing opportunities, which creates generational poverty. Then, stereotypes are now a main factor in preventing the culture from healing from this past. So, to not reinforce stereotypes, I greatly prefer to discuss the race issue in terms of either stereotypes or things like fighting poverty whenever I can (and, when applicable, I like the phrase English language learner). The word racism is just too political and sensational and doesn't address the details of the causes and effects. For example, I feel that affirmative action is a necessary evil, but public affirmative action should mostly be for people in poverty and from neighborhoods with bad schools regardless of race (much like how raising minimum wage is a public act that benefits all people of poverty equally), and should be done in a way that the decisions do not even know the race of the person (such as redacting names and pronouns). And cops who shoot unarmed people should of course lose their jobs, but let's put the emphasis on unarmed people without needing to publicly mention the race. Race only needs to be publicly mentioned when discussing how to provide better training to prevent unconscious bias or when there is an obvious or explicit racial motivation. The racism must be obvious (for example, some efforts to disenfranchise poor people or disenfranchise any small region that votes in an unwanted way is made overly dramatic in the media by focusing on racism, which distracts us from the effect of citizens being disenfranchised). We can then help poverty by doing a few simple things. For example, since having unwanted children is highly correlated with poverty and lack of success, the government should provide free birth control to everyone, especially places of poverty. This is far cheaper in the end than having to deal with a country of unwanted children and should lower legal or illegal abortion rates. And, in case you're wondering, abstinence-only education is statistically a complete failure (which is easy to understand with a basic understanding of psychology or of education). In the end, there still may be a small achievement gap between races due to different cultures having different priorities and due to how being in a minority group is inherently more challenging. I suppose that having some achievement gap is only natural, but the goal is for no one to be able to rightfully blame the system. Then, once the public side is working, it's up to our own individual choices to make all people and cultures feel welcome.
There are so many political issues that have answers if we are just willing to think statistically and carefully rather than listen to the media (or to the politicians who all participate in a popularity contest just like the media). The race issue (and the poverty issue!) is not unique in having logical solutions. The fundamental weakness of a democracy is having a population made up of people who all have naturally stupid brains. The solutions are often known by those who think statistically and carefully, but getting these solutions accomplished is the tricky part. If we think statistically, we can become part of the solution rather than the problem.
Interestingly, the United States has learned, by its completely failed attempts at establishing democracies in other countries, that meddling is very unwise. Thinking about the challenges of having a democracy just mentioned (there are other challenges too, especially when a foreign power is interfering), we should not be surprised that the Iraq and Vietnam Wars ended with such death and destabilization.
If we think statistically, we can quickly ignore the many stories in 24-hour news channels about a single person who did something stupid. Everyone sits around saying how stupid the person is for saying or doing whatever they did when all their viewers obviously agree. Like what Jerry Springer's show does! The problem with stories like this is that they are statistical outliers of no value. To make it worse, the media often portrays these cases as being typical beliefs or actions of the other side. So worse than Jerry Springer! People who think statistically ignore extreme people whenever possible.
Clearly, we can waste lots of time, effort, and money on silly things if we are easily influenced by the media rather than thinking statistically. We must not let one or two sensational stories trick us into believing that there is an actual problem. Yes, a very harmful thing such as a dirty bomb can cause many deaths at once, but this number must be compared to accumulated numbers of other causes over many years. We must not forget that a group of people dying in a sensational way is to be compared to millions dying in violent ways every year (of course, if you are the one who died, then the statistics do not matter!).
We must learn to ask good statistical questions and search for their answers. We must not just acquire our view of the world based on the TV news channel our family prefers. We must not believe a single scientist on TV or the Internet over the majority of scientists. We have to do some research. When we research, our Internet search should often include words like statistics in them.
This is a fun game to play to demonstrate another difficult aspect of getting to the important truth: fake news (not to be confused with "fake news"). In the game, you have to say whether or not a story (with information from the source) is fact or fake. You will soon learn that fake often sounds very true! If you are wondering if the game itself is fake news, good for you! The answer is that a research group at American University created the game, and you may always research the game's answers further.
In addition to the media, casinos also take advantage of the shortcomings of the human brain. Ignoring the addictive aspect of gambling (the brain's dopamine/reward centers respond greatly to random rare rewards, the brain remembers wins more than losses, etc.), many gamblers are simply bad at statistics. Most gamblers do not understand the true nature of random chance, as described by the gambler's fallacy and the hot-hand fallacy. All gamblers will fall prey to gambler's ruin, and many fall prey to gambler's conceit. Even if you do not care to think about the statistics in these links, just know that the statistics are all against you. Do you want to be an example of the brain's stupidity by letting casinos trick you out of your money? Just play games of chance for free at home! People who think statistically do not gamble (unless they are statistical geniuses who can count cards and get away with it!).
Scientific papers are often wrong. I am trusting you to think about this statement critically before rejecting science. Here is a great video describing the situation (watch it!). Keep in mind that the scientific method gets things correct far more often than any other method. Scientists are typically aware of the problem, so, unlike the media and its viewers, they know how to interpret the results of papers (scientists are much harder to convince of something after reading a peer-reviewed paper or two than the media and its viewers). Think of scientific papers as letters written between scientists not intended to be seen by the public as they can be misinterpreted.
Here is another great link showing true data that seems to suggest hilarious things! These situations demonstrate that if we look at a million pairs of things, some of them will by chance show a correlation! However, these correlations usually do not imply any causal connection. After all, given the vast number of pairings, "miracles" are common! This is a primary reason why many scientific papers are not correct: the papers are describing a "miracle" that has no causal connection. Luckily, the fields of theoretical physics and math are immune from this problem because they use deductive reasoning rather than inductive reasoning. Other fields are somewhat immune because they use statistical methods to reduce the certainty of a result according to how many different ways of "slicing" the data were explored.
As for pure incompetence or corruption, this happens too. Medical research especially has this problem, even with randomized trials, perhaps because of how much money can be made in medicine. There is especially a problem with research from certain countries that lack sufficient infrastructure and regulations, though any institution has some degree of incompetence. If it helps us feel better, we can remind ourselves that a much larger problem in medicine is medical errors by hospitals.
So when do we believe something? Unless we are experts in a particular field whose job it is to improve our conclusions, we should believe something when the majority of scientists in the field tells us to (that is, when it ends up in a college textbook). A single sensational study, especially if in the media and especially if it is about the latest fad, should not be believed. Only an idea that has been tested repeatedly is seriously considered by the majority of the scientific community. Here is a great example of a ridiculous claim by the media that many scientists immediately knew to be ignorant.
When working out actual problems when doing scientific research or trying to understand some statistical results, much time is often spent thinking very carefully about what is the exact statistical question and how to interpret the statistical answer. This is because we often do things wrong the first time, so we must double and triple check ourselves.
Let's take the above Birthday problem as an example for the remainder of this discussion. For N people in a room, there are
(N-1) + (N-2) + (N-3) + ... + 1 + 0
= N (N-1) / 2
unique pairs of people. On the first line, the first term is the number of pairs with an arbitrary person, the second term is the number of unique pairs for the next person, etc. (the final person has no more unique pairs as every other person has paired with them). The second line is from adding up the numbers. The large number of pairs is why the probability that two people have the same birthday is so surprisingly high. Let's now work out, given N, what the probability is that two people have the same birthday. Let's do this to show how we are often wrong at first. For simplicity, we will ignore leap years, twins, some months being more likely to have birthdays, etc.
If N = 1, then there are 0 pairs, so probability is 0 to have 2 people having the same birthday.
If N = 2, then there is 1 pair, so there is a 1/365 probability that one person has the same birthday as the other person.
If N = 3, then there are 3 pairs. Given any pair, there is a 1/365 probability of having the same birthday. But what are the chances of there being at least one pair in the room with the same birthday?
Our very first guess is that
probability = 1/365 + 1/365 + 1/365
This guess is clearly wrong if the number of pairs is larger than 365 (when N > 27), so we immediately reject this formula. However, the formula is approximately correct for small N. A reason that this formula is wrong is that the effects of each pair after the first are dependent on the results of the previous pairs. For example, if the first two pairs considered had the same birthday, all 3 people must have the same birthday, so the third and final pair must also have the same birthday.
Our next idea is that, after the first pair, each following pair increases the remaining probability, 1 - probability, giving the following algorithm...
probability1 = 1/365
probability2 = probability1 + 1 / 365 * (1 - probability1)
probability3 = probability2 + 1 / 365 * (1 - probability2)
The subscript tells us the pair being considered. The idea is to make the effect of pairs dependent on the previous ones. This idea is approximately the same as the very first guess when N is small, and probability never exceeds 1 if N is very large, which was the whole point of this approach. However, it never equals 1, as it must when N > 365. So even this more clever and more accurate approach is wrong. Educated guessing can be a useful tool, but this formula was only a guess. The effects of each pair being dependent on the previous pairs must be more complicated than this simple formula captures.
While thinking about the number of pairs was very helpful in making sense out of the high-probability results of the Birthday problem, finding the correct mathematical formula should not consider pairs. I would assume that many people not well trained in statistics would try to solve this problem using pairs, but this is incorrect. Instead, let us consider people because we assumed that the birthdays of each person are not dependent upon the other people. When things are not dependent, we can use the following simple rules: (1) probabilities multiply if actions are done at the same time or in succession and (2) probabilities of (mutually exclusive) alternatives add. Pairs do not follow the first rule because they are dependent.
For our N = 3 situation, let us say that one person has birthday A. If the next person has the same birthday, it is also A, else B. So, there are the following possibilities...
A A A
A B B
A B A
A A B
A B C
The probability that the second person is the same as the first is 1/365, and the probability that they are different is 364/365. For each of the above possibilities, rule (1) says that we must multiply the probability of the third person's result to this, giving...
A A A (1/365) * (1/365)
A B B (364/365) * (1/365)
A B A (364/365) * (1/365)
A A B (1/365) * (364/365)
A B C (364/365) * (363/365)
Rule (2) says that we can add up these probabilities, and, when we do this, we get 1! That is, we can expect the above possibilities to occur 100% of the time because it is a complete list. However, alternative A B C is the only alternative that does not give the result of two people sharing a birthday, so we get
probability = 1 - (364/365) * (363/365) = 0.008204 = 0.8%
This is the correct answer!
We may generalize this formula. For example, if N = 4, only A B C D has no two people sharing a birthday, so
probability = 1 - (364/365) * (363/365) * (362/365)
Generalizing even further gives
probability = 1 - (364/365) * ... * ((366 - N) / 365)
When N = 365, the formula gives that there is a 1 - 1.7 × 10-157 probability of there being a pair. For N > 365, the formula gives exactly 1 as expected! If we were wondering if a room will have three people with the same birthday, generalizing the formula for large N would be a much harder task.
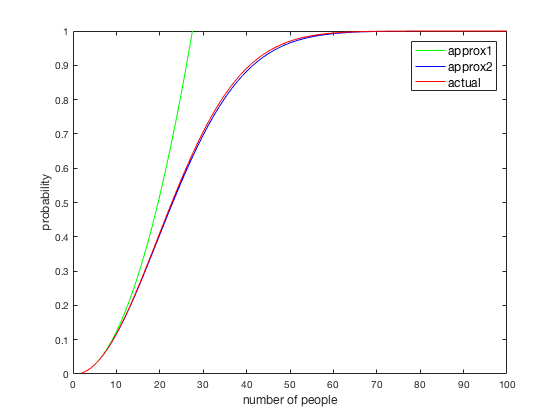
So how do our methods perform? In the figure below, the first method is the naive adding of probabilities (approx1). The next method is for the improvement to this method (approx2). Finally, the correct probabilities are show (actual). For very small N, all methods approximately agree and show a fast increase in probability. Note that, for N > 27, the first method fails altogether.

Yes, getting the correct answers is often this difficult!
For a harder example, you may wish to solve the following problem. I Googled around and I could not find the solution, so this should be a sufficiently hard one to test our problem solving. The problem is similar to the coupon collector's problem, but the solution is very different (unlike the coupon collector's problem, we now have more information because we have collected our "coupons" already, but we do not know how many types of "coupon" there are).
Problem: Your friend is spinning a prize wheel with k locations. Each location has a unique prize and is equally likely to be landed on. You cannot see the wheel, but a loudspeaker calls out the prize after each spin. After N spins, you want to know the probability that the wheel has hit every location at least once. That is, you are trying to get a complete list of possible prizes, and you want to know if stopping is reasonable. Of course, for even very large N, you can never be completely certain that everything has been found, so you want to know how likely it is that everything has been found. Make no assumptions about the size of the wheel. That is, before any spins, it is equally likely to have k = 1 or k = 1,000,000 (this is called assuming a uniform prior). In the case that you get 4 unique prizes 2, 3, 1, and 3 times, respectively, calculate the probability that you are finished.
Answer: I get 37%, so you should keep waiting for more spins of the wheel! If you are wondering what the chances of there being a single prize left, this is 25%. The probability of there being two prizes left is 14%. The probability of there being more than 5 prizes left is 7%. If you get an answer, send me a message! If you are incorrect, I can give you a large number of hints if you describe what you did. You may also look at the source of this .html file to view HTML comments containing the answers.
Hints to get you started: First of all, N = 2 + 3 + 1 + 3 = 9, and define kmin = 4 since the minimum number that k can be is 4. Look into something called the multinomial distribution. First, derive a formula and method for finding the answer. Then, test this method on simple cases to see if it gives correct results. For example, if getting a unique prize every time, you should always calculate exactly 0% chance that you are finished. In fact, for the probability to be nonzero, my results show that N - kmin > 1 is necessary and sufficient. Since realistic wheels cannot have any of in infinite number of prizes, this 0% is not realistic. Luckily, nonzero probabilities typically are affected only a small amount by the very-large-k possibilities, so nonzero probabilities you calculate are likely realistic.
Crucial conceptual hint: The key to this exercise is to realize that probability cannot depend on details that are irrelevant to the question being asked. When asking if the search is finished, one does not care about which exact prizes are won. All possible unique ways of getting 2 3's, a 2, and a 1 for the counts are what we care about (we don't care about the exact prizes obtained). Carefully understanding the multinomial distribution should give you a way of multiplying your results by the number of unique ways. If you do not consider all unique ways, the probability of being finished is artificially high simply because landing on the exact 4 prizes becomes very unlikely for large k. By the way, if this all seems very subtle and complicated, it is! Realizing that statistics is tricky is the whole point of everything I have written here!
Alternative solution: You may attempt to use the multiplication and addition rules that were used in the Birthday problem above. This will be very tedious to directly solve our problem, and, even if it were done, the result would be of little worth because the tedium would have to be repeated after each spin of the wheel when updating the probabilities. What we really want is to come up with a formula generalized from simpler problems. We can then apply this formula to the exact problem at hand. To get an idea of what this formula could be, let's consider the much simpler problem of getting a prize twice, and getting two other prizes once (so N = 4). For k = kmin = 3, you should get
probability = (3/3)*(1/3)*(2/3)*(1/3) + (3/3)*(2/3)*(2/3)*(1/3) + (3/3)*(2/3)*(1/3)*(3/3)
= (3/3)*(2/3)*(1/3)*(6/3)
and for k = 100 you should get
probability = (100/100)*(1/100)*(99/100)*(98/100) + (100/100)*(99/100)*(2/100)*(98/100) + (100/100)*(99/100)*(98/100)*(3/100)
= (100/100)*(99/100)*(98/100)*(6/100)
Now factor out the 6 from each of these answers, and write the rest in terms of N, k, and kmin using factorials when necessary. Try another N to see if your formula still holds true. Then think about how to use this formula to compare different k's to calculate the final answer.
Final question: It is very possible that, in the next spin, you now have 5 unique prizes 2, 3, 1, 3, and 1 times, respectively. The probability of being finished is now 22%, which is down from 37% even though the probability of being finished is expected to increase as more spins are performed (eventually, all the prizes will have been found multiple times). The question is this: should you use the previous 37% to feel more confident than the more recent 22%? The answer is that the only important probability is now the 22%. By its nature, probability tries to quantify what we do not know, so probability can increase or decrease as more is learned. We should always obtain and use the largest data set possible so that our probabilities reflect more knowledge and less unknown, just be sure to include all data else things become more complicated.